ជាការសាកល្បងលើគណិតវិទ្យានិងបញ្ហាលំបាកពីសម័យអេហ្ស៊ីបត្រូវបានបង្ហាញបន្តិចម្តងៗពិសេសគណិតវិទ្យាដែលអ្នកប្រាជ្ញគណិតវិទ្យាគ្មានសមត្ថភាពស្រាយជូនត្រូវបានបញ្ញាសិប្បនិម្មិត (Artificial Intelligence) ឬហៅថា AI ស្រាយបានយ៉ាងងាយ។
យោងតាម IFL Science ល្បែងផ្គុំរូបដែលមានអាយុកាលរាប់ពាន់ឆ្នាំត្រូវបានឌិកូដដោយគណិតវិទូ Thomas Bloom ហើយបង្ហោះនៅលើទំព័រផ្ទាល់ខ្លួនរបស់លោក។ ពីមុនកំណែគណិតមួយផ្សេងទៀតនៃបញ្ហានេះក៏ត្រូវបានបង្កឡើងដោយគណិតវិទូពីរនាក់គឺ Erdős និង Graham ហើយបានផ្តល់រង្វាន់ 500 ដុល្លារ ដល់អ្នកដែលអាចដោះស្រាយវាបាន។
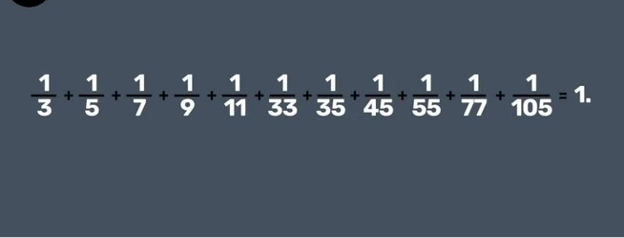
បញ្ហាត្រូវបានផ្ដល់ជូនដូចខាងក្រោម៖ ដោយផ្តល់សំណុំនៃចំនួនគត់វិជ្ជមាន ពីសំណុំនេះ តើអ្នកអាចជ្រើសរើសធាតុដែលផលបូកបញ្ច្រាសស្មើនឹងចំនួនគត់គឺ១បានទេ? ដើម្បីនិយាយឲ្យសាមញ្ញ យើងមានសំណុំ {2, 4, 6, 8, 10, 12}។ សំណួរគឺថាតើអ្នកអាចរកឃើញលេខដែលផលបូកគឺ ១ ដែរឬទេ។
ទន្ទឹមនឹងនេះ បញ្ហាបំរែបំរួលរបស់អ្នកគណិតវិទ្យាទាំងពីរ គឺលោក Erdős – Graham គឺ៖ ប្រសិនបើសំណុំ A ជាសំណុំរងនៃសំណុំ N និង A មានដង់ស៊ីតេវិជ្ជមាន មានសំណុំរង S នៃ A ដែលផលបូកនៃធាតុរបស់វាស្មើនឹង ១? ឧទាហរណ៍ ជាមួយនឹងសំណុំរងនៃ N ដែលមានដង់ស៊ីតេវិជ្ជមាន A = {3,5,7,9,11…} យើងអាចទទួលបានចំនួនច្រើនគ្រប់គ្រាន់នៃចំនួនធម្មជាតិជាប់ៗគ្នាដែលមានប្រូបាប៊ីលីតេនៃអត្ថិភាពថាតើចំនួនមួយជាកម្មសិទ្ធិ ទៅ A ខុសពី 0 ឬអត់ ?។
សំណួរនេះស្តាប់ទៅសាមញ្ញ ប៉ុន្តែអ្នកគណិតវិទូខ្លះនិយាយថា បញ្ហានេះគឺ «ពិបាកបំផុតមិនធ្លាប់មាន»។ គណិតវិទូ Andrew Granville នៃសាកលវិទ្យាល័យ Montreal ប្រទេសបារាំង បានឆ្លើយប្រាប់ ទស្សនាវដ្តី Quanta ថា “ខ្ញុំគិតថា នេះជាបញ្ហាដែលមិនអាចទៅរួច ដែលគ្មាននរណាម្នាក់អាចដោះស្រាយបាន។ ខ្ញុំមិនឃើញឧបករណ៍ច្បាស់លាស់ណាមួយដែលអាចដោះស្រាយបាននោះទេ»។ ទោះជាយ៉ាងណាក៏ដោយ លោក Bloom បានរកឃើញចម្លើយដោយចៃដន្យនៅក្នុងអត្ថបទមួយកាលពី ២០ ឆ្នាំមុន ដែលបានបោះពុម្ពនៅក្នុងសៀវភៅ Annals of Mathematics ឆ្នាំ ២០០៣ ដោយគណិតវិទូ Ernie Croot ។
អ្វីដែលលោក Croot បានដោះស្រាយត្រូវបានគេហៅថា “កំណែពណ៌” នៃបញ្ហា Erdős – Graham ។ ដោយសារតែវាពាក់ព័ន្ធនឹងសំណុំរង “ពណ៌” វាស្រដៀងទៅនឹងការបែងចែកសំណុំ A ដោយយកធាតុ A ទៅក្នុងចំនួនកំណត់នៃប្រអប់ដែលមានពណ៌ខុសៗគ្នា។
បន្ទាប់មក លោក Bloom បានអនុវត្តគំនិតរបស់ Croot ហើយបានដោះស្រាយបញ្ហាលំបាកទាំងស្រុង។ លោកជឿថា Croot បានបង្ហាញពីករណីពិសេសនៃបញ្ហានេះ។ “វិធីសាស្រ្តរបស់ Croot គឺពិតជាមិនធម្មតា លោកសមនឹងទទួលបាន ៩៩% នៃចំនួនអសនិទាន។ អ្វីទាំងអស់ដែលខ្ញុំបានធ្វើនិងស្រាយមកនេះដើម្បីបញ្ចប់បញ្ហាដែលមានយូរណាស់មកហើយតាមលទ្ធភាព ម៉្យាងពេលទៅឃើញរូបភាពគ្មានអ្នកបកស្រាយជូនពិភពលោក។
តាមគំនិតរបស់លោក Bloom គឺថា ជំនួសឱ្យការស្វែងរកលេខដែលផលបូកបញ្ច្រាសគឺ ចំនួនគត់លេខ១យើងរកលេខដែលផលបូកតូចជាង បន្ទាប់មកបន្ថែមទៅ១។ ឧទាហរណ៍ យើងអាចស្វែងរកក្រុមដែលផលបូកបញ្ច្រាសគឺ ១/៣ តាមវិធីផ្សេងៗគ្នា។ លោក Bloom បានប្រាប់ថាទោះជាមិនបានលទ្ធផលតាមតែយើងចង់បានកី្តតែវាបានបញ្ជាថា បញ្ញាសិប្បនិម្មិត (Artificial Intelligence) ឬហៅថា AI សិក្សាពង្រីកសមត្ថភាពខ្លួនបន្តទៀត៕